LogisticRegression

Machine Learning

谈到机器学习算法，从理解上来说，就是从已经有的数据首先要谈到监督学习和非监督学习。

监督学习，定义是利用一组已知类别的样本调整分类器参数，使其达到所要求性能的过程。这个理解很简单，就是我们通过算法面试，需要做一些算法题，如果有答案，我们就知道自己做的对不对，这样自己的结果有对照，那样在面对新的算法题的时候，我们虽然不会碰到原来的题目，但是通过原来算法题的训练，做出题目的概率会更高。在机器学习中，监督学习就是分类，通过输入数据的特征和标签，找到特征和标签之间的映射关系。这样拿到新的有特征但是没有标签的数据，我们可以通过已有的数据进行监督学习来得到未知数据的标签。

非监督学习，定义是在未加标签的数据中，试图找到隐藏的结构。这个相对于监督学习就是并没有标签，我们理解标签可以是已有数据的已有判定结果。对比在通过算法面试上，就是我们并没有标准答案，而是需要自己去根据不同的算法题去摸索出特征和结果。在机器学习中，非监督学习就是聚类。

除了监督学习和非监督学习，当然还有半监督学习，即部分数据有特征和标签，部分数据没有标签。因为要让所有数据都有标签是一件困难的事情，所以现在最热门的是半监督学习。

Classification

谈到逻辑回归模型，首先就需要谈到线性回归模型，这里先解释一下回归和分类的含义，在Andrew Ng的Machine Learning中的定义是：
Supervised learning problems are categorized into “regression” and “classification” problems. In a regression problem, we are trying to predict results within a continuous output, meaning that we are trying to map input variables to some continuous function. In a classification problem, we are instead trying to predict results in a discrete output. In other words, we are trying to map input variables into discrete categories.
即二者的区别主要在于输出结果是否连续。分类输出的是离散数据，回归输出的是连续数据。所以Logistic Regression其实是一种分类算法而不是回归算法，只是中间用到了回归算法，其输出的结果是决策边界。

Linear Regression

线性回归的定义是，利用数理统计中的回归分析，来确定两种或者两种以上变量之间相互依赖的定量关系的一种统计分析方法。根据回归分析中存在的自变量个数，分为一元线性回归分析和多元线性回归分析。
首先，我们需要明确的一点是，我们要解决什么问题需要用到逻辑回归，已有的线性回归在哪里是不够用了。在进行分类问题的运算过程中，我们会碰到很多的二分类问题，例如邮件是否为垃圾邮件、在线交易是否有欺诈行为等。

1.对于二分类问题，我们只需要两个结果，0称为负例，1称为正例。线性回归模型的假设输出值$ h_θ(x) = θ^TX$，可能大于1，也可能小于0。不符合我们二分类的要求，需要一个假设位于0和1之间的假设，那么逻辑回归就满足这个条件。
2.逻辑回归源于线性回归，逻辑回归本质上是一个线性回归模型，因为除了逻辑回归主要使用的sigmoid函数，其他的步骤，逻辑回归和线性回归都一样。只不过线性回归无法做到sigmoid的非线性形式。
3.如果用线性回归来拟合逻辑回归函数数据，就会形成很多局部最小值，构成一个非凸集。而线性回归的损失函数是一个凸函数，那么就和模型不符合。
4.其实可以将逻辑回归理解为被归一化的线性回归。

Logistic Regression

逻辑回归的因变量可以是二分类的，也可以是多分类的。但是二分类的场景更为常用，因此在实际的工作中，用的最多的就是二分类的逻辑回归。首先介绍sigmoid函数：
$$
g(z) = {1 \over {1 + e^{-z}}}
$$

Classifier

在拿到sigmoid函数的时候，第一反应就是为什么要用这个函数？首先需要引入线性分类器的概念。对于一般的二分类问题来说，我们需要找到一个线性分类器，来将这些数据分为两类。即线性分类器就是找到一个超平面，将两类样本分开。线性分类器中，最简单的就是感知器，感知器就是将所有特征和权重做内积，然后根据和阈值大小的比较，将样本分为了两类。感知器就相当于在《信号与系统》中学习的阶跃函数，阶跃函数简单易懂，就是通过划定一个阈值，比较样本与阈值的大小来进行分类。

这个阶跃函数就能实现二分类的需求。但是有一个很大的问题是，阶跃函数并不是一个光滑的函数模型，在阶跃点的处理上，到底是属于0还是1，没有一个合理的判断标准，于是，就出现了sigmoid函数，它的优点是:

1.输入范围(-∞,+∞)，输出范围(0,1)，均满足分类器的要求。
2.具有良好的连续性，不存在不连续的点。

Cost Function

在李航《统计学习方法》中阐释过，方法=模型+策略+算法，策略最常用的方法就是损失函数(cost function)，cost function是评价回归模型是否拟合训练集的方法，如果值越小，说明模型越好。

如果还有点抽象的话，就是说我们通过最大似然估计、最大后验证概率或者最小化分类误差等建立模型的损失函数，通过求解这个损失函数的最小值，找到最优解。

常见的损失函数有0-1损失函数、平方损失函数、绝对值损失函数、对数损失函数。在逻辑回归中用的损失函数是对数损失函数。

Maximum Likehood Estimate

最大似然估计有很多种官方解释，其中一个解释就是拿到了很多样本，这些样本值已经实现，最大似然估计就是从这些样本值的结果信息中推算出来最有可能产生这些样本值的模型参数值。

这里有一个很直观的例子，从一个有足够黑球和白球的罐子里有放回的拿出100个球，其中50个黑球，50个白球，请问这个罐子里黑球的比例最有可能是多少？

答案当然是50%，那这个问题背后的数学知识是什么？我们假设黑球的比例是p，那么白球的比例就是1-p，这里100次取球中黑球50，白球50的比例是
$$
P = {p^{50}} * {(1-p)^{50}}
$$
如果要P的值最大，两边同时去ln，可以发现当p = 50%时候，P最大。
即最大似然估计就是在一个大的参数样本中，我们无法马上得出大样本分布的参数值，可以通过采取小样本的估计方法，来获得大样本分布中的参数值。

Evaluation

逻辑回归常用的二分类性能评估指标为：

True Positive(TP)，被模拟为正的正样本
True Negative(TN)，被模拟为负的负样本
False Positive(FP)，被模拟为正的负样本
False Negative(FN)，被模拟为负的正样本
精确率，衡量判断出来的正样本中正样本的真实比例，也称为TPR(true positive rate)，查准率，公式为：$precision = {TP \over {TP + FP}}$
准确率，衡量整个分类器的衡量能力，公式为：$accuracy = {(TP + TN) \over (TP + FN + FP + TN)}$
召回率，衡量判断出来的正确的正样本在所有正样本中的比例，也称为查全率，公式为：$recall = {TP \over {TP + FN}}$，也称为TPR
- 一般查准率(precision)和查全率(recall)是负相关，原因是：两者的分母相差的就是FP和FN的不同，可以这么理解，因为FP是0判1，FN是1判0，当你把大量样本的0判定为1了之后，响应的1判定为0的样本就很少，这样两者必然负相关，两者经常绘制PR曲线为：
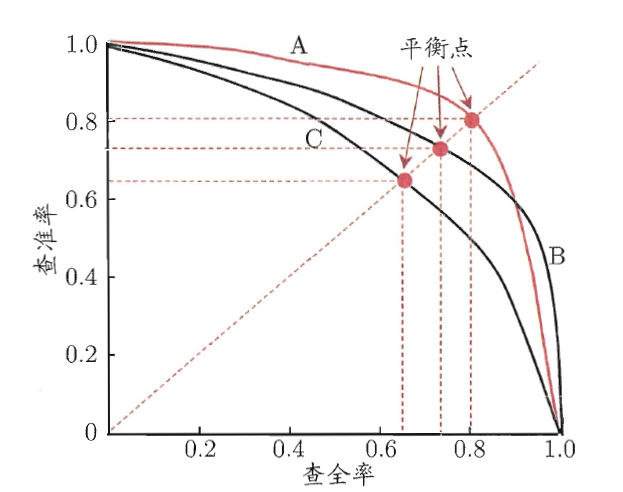
- 如果一个模型的PR曲线被另一个模型的PR曲线包住，说明另一个模型的效果更好。如果两个模型的PR曲线相交，就得具体分析其他的指标。
F度量，简单理解为precision和recall的调和平均值，公式为：$F = {2(precision * recall) \over (precision + recall)}$，即综合两个指标的评估的综合反映。
ROC曲线，先要介绍TPR和FPR
- TPR，真阳性率，即所有正样本中，判断正确的正样本的比例，和recall计算公式一样，公式为：$TPR = {TP \over {TP + FN}}$
- FPR，假阳性率，即所有的负样本中，判断错误的负样本比例，公式为：$FPR = {FP \over {FP + TN}}$
- ROC曲线横坐标是FPR，纵坐标是TPR。考虑ROC曲线的四个点，(0,1)是FPR = 0，TPR = 1，这意味着FN = 0，FP = 0，这里是将所有的样本都正确分类。(1,0)是FPR = 1， TPR = 0，这意味着TN = 0， TP = 0，这里是将所有的样本都错误分类。(0,0)是FPR = 0，TPR = 0，这意味着TP = 0， FP = 0，这意味着预测的都是负样本。(1,1)是FPR = 1， TPR = 1，这以为着预测的都是正样本。那么ROC曲线越接近左上角，意味着预测的效果越好。
- 这里如何绘制ROC曲线就需要提出一个threshold的概念，何为阈值，因为我们判定TP、TN、FP、FN都是根据一定的阈值来判定自己是否判定正确。尽量取更多的threshold值，那样ROC曲线可以更平滑。
AUC值，AUC值是ROC曲线下的面积，显然这个面积的数值不会大于1，因为ROC曲线一般都在y = x的上方，AUC取值一般都为0.5-1之间，一般AUC的值更大说明分类效果更好。

Summary

在代码执行这一块，比如用Logistic Regression来说，用Python来调用，其实就是一个黑盒操作，理解其中的原理还是十分重要的。

Example

Procedure

现在有一个应用场景，有一些用户的银行数据，通过这些银行数据来判断是否给该用户批准信用卡。用户的特征有：年龄、性别、借记卡数量、信用卡数量、最近一个月，两个月，三个月的平均消费、最近一个月的收入，用户的结果就是是否批准信用卡，在这里的场景下是fraud = 0，说明不是适宜客户，不批准；fraud = 1，说明是适宜客户，批准。
首先看一下，训练集和测试集的内容

import pandas as pd
import numpy as np
d01 = pd.read_csv('../d_train.csv',encoding='utf-8')
d02 = pd.read_csv('../d_test.csv',encoding='utf-8')
d01.describe()

可以看到这里对于训练集的一些统计信息，发现age和consume1m的个数有差异，说明consume1m的内容有空值，那么开始一个简单的处理：

d01['consume1m'].isnull()
d01['consume1m'].notnull().describe()
d01['consume1m'].fillna(0,inplace=True)
d01['consume3m'].fillna(d01['consume3m'].mean, inplace = True)
d01.dropna(how='any',inplace = True)
d01['consume1m'].isnull().describe()

我们可以通过metplotlib来找出箱线图，观察数据的分布，年龄是重要的特征，那么来看看年龄的分布：

%matplotlib inline
import matplotlib.pyplot as plt
plt.boxplot(d01['age'])
plt.show()

show:

可以看出平均的年龄分布，最大值和最小值。我们通过分析数据得到income1m的特征里面有个值显得特别大，这样特别大的值会影响模型的效果，我们就要把这个值给去除。另外对于性别和贷款与否都可以用0和1来表示，而age这个特征值可以通过分段将定量转为定性的分布。另外经验表示，训练集和测试集的样本个数一样的话，分类效果更好，样本处理如下：

m = d01['income1m'].max()
d01 = d01[(True^d01['income1m'].isin([m]))]
n_good = len(d01.fraud[d01.fraud==1])
n_bad = len(d01.fraud[d01.fraud==0])
d_good = d01[d01.fraud == 1]
d_bad = d01[d01.fraud == 0]
l_good = np.random.choice(range(n_good),size=n_bad,replace=False)
l_good = l_good.tolist()
d_good_new = d_good.iloc[l_good]
d01_new = pd.concat([d_good_new, d_bad], axis = 0)
d01 = d01_new
y1 = d01['fraud']
y2 = d02['fraud']
d1 = d01.drop(['fraud'], axis = 1, inplace = False)
d2 = d02.drop(['fraud'], axis = 1, inplace = False)
d1['loan'] = d1['loan'].replace(['no','yes'], [0, 1])
d2['loan'] = d2['loan'].replace(['no','yes'], [0, 1])
d1['sex']=d1['sex'].replace(['F','M'],[0,1])
d2['sex']=d2['sex'].replace(['F','M'],[0,1])
d1['age1'] = (d1.age<30)
d2['age1'] = (d2.age<30)
d1['age2'] = (d1.age<50)
d2['age2'] = (d2.age<50)
d1.drop(['age'],axis=1,inplace=True)
d2.drop(['age'],axis=1,inplace=True)
d1.head()

下面就开始对数据的预处理，我们引入sklearn。对于不同量级的数据，要进行标准化和归一化的操作，标准化是去除均值和方差缩放，标准化sklearn有两种方式，1.用sklearn.preprocessing.scale()函数，可以直接将给定数据进行标准化;2.使用sklearn.preprocessing.StandardScaler类，类的好处是保存训练集参数直接用对象转换测试集数据。归一化是将属性缩放到一个指定的最大值和最小值之间，可以通过processing.MinMaxScaler实现，这里对于方差很小的属性可以增强稳定性，并维持稀疏矩阵中为0的条目。

from sklearn.linear_model import LogisticRegression
from sklearn import preprocessing
scaler = preprocessing.StandardScaler().fit(d1)
x1 = scaler.transform(d1)
x2 = scaler.transform(d2)
min_max_scaler = preprocessing.MinMaxScaler()
x_train = min_max_scaler.fit_transform(x1)
x_test = min_max_scaler.fit_transform(x2)
lr = LogisticRegression()
lr.fit(x_train, y1)

下面开始检验测试集

1 2	y_pre = lr.predict(x_test) y_pre

Analyse

观察一下分类准确率：

from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
accuracy_score(y2, y_pre)

结果是0.91666666666666663，观察TP、TN、FP、FN值：

1
2
3

from sklearn.metrics import confusion_matrix
confusion_matrix = confusion_matrix(y2, y_pre)
print (confusion_matrix)

结果是：
[[105 10] [15 170]]
观察一下准确率：

from sklearn.metrics import precision_score
y_true = np.array(y2)
y_pred = np.array(y_pre)
precision_score(y_true, y_pred)

结果为0.94444444444444442，观察召回率：

from sklearn.metrics import recall_score
y_true = np.array(y2)
y_pred = np.array(y_pre)
recall_score(y_true, y_pred)

结果为0.91891891891891897，观察F1值:

from sklearn.metrics import f1_score
y_true = np.array(y2)
y_pred = np.array(y_pre)
f1_score(y_true, y_pred)

结果为0.93150684931506844，观察AUC值：

from sklearn import metrics
y_true = np.array(y2)
y_pred = np.array(y_pre)
fpr, tpr, thresholds = metrics.roc_curve(y_true, y_pred)
metrics.auc(fpr, tpr)

结果为0.91598119858989424。

Summary

这个模型有较好的学习效果，也看出了逻辑回归的良好应用，做一个模型就要把模型的每个点都要搞透，贪多嚼不烂。